As tolerâncias dimensionais estabelecem a base para a qualidade e o desempenho dos equipamentos de tubos de quartzo de laboratório. Os engenheiros percebem que mesmo pequenas alterações no diâmetro, na espessura da parede, no comprimento ou na retidão do tubo de quartzo podem alterar a qualidade da vedação a vácuo, do controle térmico e do alinhamento óptico. Quando as tolerâncias são insuficientes, os laboratórios enfrentam problemas de desempenho dispendiosos e menor confiabilidade do equipamento. Os tubos de quartzo de alta qualidade com tolerâncias precisas mantêm resultados consistentes e ajudam os laboratórios a controlar os custos. O equipamento correto de tolerâncias dimensionais para tubos de quartzo de laboratório garante que cada integração atenda aos rigorosos padrões de qualidade e desempenho.
Principais conclusões
As tolerâncias dimensionais são cruciais para garantir a qualidade e o desempenho dos equipamentos de tubos de quartzo de laboratório.
A manutenção de uma tolerância de ±0,2 mm no diâmetro externo é essencial para uma vedação a vácuo confiável e uma compressão ideal do anel O-ring.
A espessura uniforme da parede de ±0,1 mm evita pontos quentes e garante a distribuição uniforme do calor em fornos de laboratório.
A tolerância de retidão de menos de 0,5 mm por 500 mm é vital para o alinhamento óptico preciso e para minimizar a perda de sinal.
Os engenheiros devem usar a análise de tolerância estatística para prever variações de montagem e melhorar o sucesso da integração.
Como a tolerância de ±0,2 mm de diâmetro externo permite a integração de fornos selados a vácuo?

As tolerâncias dimensionais desempenham um papel crucial na integração de tubo de quartzo para laboratório equipamento de tolerâncias dimensionais. Uma tolerância precisa de ±0,2 mm no diâmetro externo (DE) garante que os tubos de quartzo se encaixem perfeitamente nos sistemas de fornos selados a vácuo. Esse nível de controle garante vedação confiável, desempenho consistente e resultados de alta qualidade em instrumentos analíticos.
Cálculo da compressão do anel de vedação: Como ±0,2 mm mantém o aperto ideal do 15-25%
Os engenheiros usam a análise de compressão do O-ring para determinar a compressão correta para vedações a vácuo. Quando os tubos de quartzo têm uma tolerância de ±0,2 mm de diâmetro externo, o anel O-ring se comprime entre 15% e 25%, o que corresponde aos padrões ISO e ASTM para a integridade do vácuo. Essa faixa evita tanto a subcompressão, que pode causar vazamentos, quanto a supercompressão, que pode danificar os tubos de quartzo de alta pureza.
A compressão do O-ring afeta diretamente a qualidade da vedação e o desempenho do sistema. Se a tolerância do diâmetro externo exceder ±0,5 mm, o anel O-ring poderá se comprimir demais, criando uma força de fixação excessiva que pode causar a fratura do tubo. Se o tubo for muito pequeno, o O-ring não vedará adequadamente, permitindo a entrada de ar e impurezas e causando contaminação. Os testes mostram que a manutenção da faixa de compressão correta mantém as taxas de vazamento abaixo de 10-⁶ std-cc/seg, o que é essencial para aplicações analíticas que exigem alta precisão e resultados confiáveis.
Pontos principais:
A compressão correta do anel O-ring (15-25%) garante a integridade da vedação a vácuo
A compressão excessiva ou insuficiente leva a vazamentos ou danos ao tubo
A tolerância precisa do diâmetro externo permite um desempenho consistente e de alta qualidade
Impacto da taxa de vazamento: ±0,2 mm atinge <10-⁶ vs. ±0,5 mm causando 10-⁴ std-cc/s
A análise da taxa de vazamento destaca a importância de tolerâncias dimensionais rigorosas. Os tubos de quartzo com tolerância de ±0,2 mm de diâmetro externo atingem consistentemente taxas de vazamento abaixo de 10-⁶ std-cc/seg, atendendo aos padrões de qualidade ISO e ASTM para sistemas de vácuo. Em contraste, os tubos com tolerância de ±0,5 mm podem apresentar taxas de vazamento tão altas quanto 10-⁴ std-cc/seg, o que permite a contaminação e reduz o desempenho do sistema.
A diferença nas taxas de vazamento afeta a integridade dos ambientes controlados. Altas taxas de vazamento introduzem impurezas que podem comprometer a pureza do SiO₂ e contaminar amostras sensíveis. A vedação confiável é essencial para o vidro de quartzo usado em instrumentos analíticos, onde até mesmo pequenos vazamentos podem afetar os resultados e exigir retrabalho dispendioso.
Tolerância (OD) | Taxa de vazamento (std-cc/seg) | Impacto na qualidade | Risco de desempenho |
|---|---|---|---|
±0,2 mm | <10-⁶ | Certificado, confiável | Mínimo |
±0,5 mm | 10-⁴ | Não confiável, não certificado | Alta (contaminação) |
Essa tabela mostra como as tolerâncias mais rígidas levam a uma melhor qualidade e a resultados mais confiáveis.
Integração do forno a vácuo: Controle da folga para confiabilidade da vedação
A análise da folga garante que os tubos de quartzo se encaixem com segurança nos orifícios do forno. Uma tolerância de ±0,2 mm no diâmetro externo cria uma folga consistente, que permite a compressão adequada do anel O-ring e evita o encaixe forçado. Esse controle permite uma instalação confiável e mantém a qualidade da vedação a vácuo.
Quando a folga é muito grande ou muito pequena, o risco de contaminação e estresse mecânico aumenta. O controle adequado da folga também ajuda a manter a precisão dos resultados analíticos, evitando vazamentos e garantindo que o sistema opere dentro de protocolos certificados. Os tubos de quartzo de alta pureza que atendem a esses padrões dimensionais suportam o desempenho de longo prazo e reduzem a necessidade de retrabalho.
Resumo dos benefícios:
As folgas consistentes protegem a integridade da vedação
O ajuste adequado reduz a contaminação e o estresse mecânico
As tolerâncias dimensionais certificadas garantem um desempenho confiável e de alta qualidade
Como a uniformidade de ±0,1 mm na espessura da parede afeta a distribuição do gradiente térmico?
A uniformidade da espessura da parede em tubos de quartzo desempenha um papel fundamental no desempenho do forno de laboratório. A espessura consistente da parede garante uma transferência uniforme de calor, o que evita pontos quentes e permite uma operação confiável. Os laboratórios dependem desse nível de controle para manter a qualidade e a precisão do processo em instrumentos analíticos.
Variação da massa térmica: Como ±0,1 mm evita a formação de pontos quentes (±3°C vs. ±15°C)
Os tubos de quartzo com uniformidade de ±0,1 mm de espessura de parede distribuem o calor uniformemente ao redor da circunferência. Essa uniformidade mantém as diferenças de temperatura dentro de ±3°C, o que evita pontos quentes que podem causar estresse térmico e falha do tubo. Quando a espessura da parede varia em mais de ±0,25 mm, as diferenças de temperatura podem chegar a ±15°C, causando rachaduras e reduzindo a vida útil do equipamento.
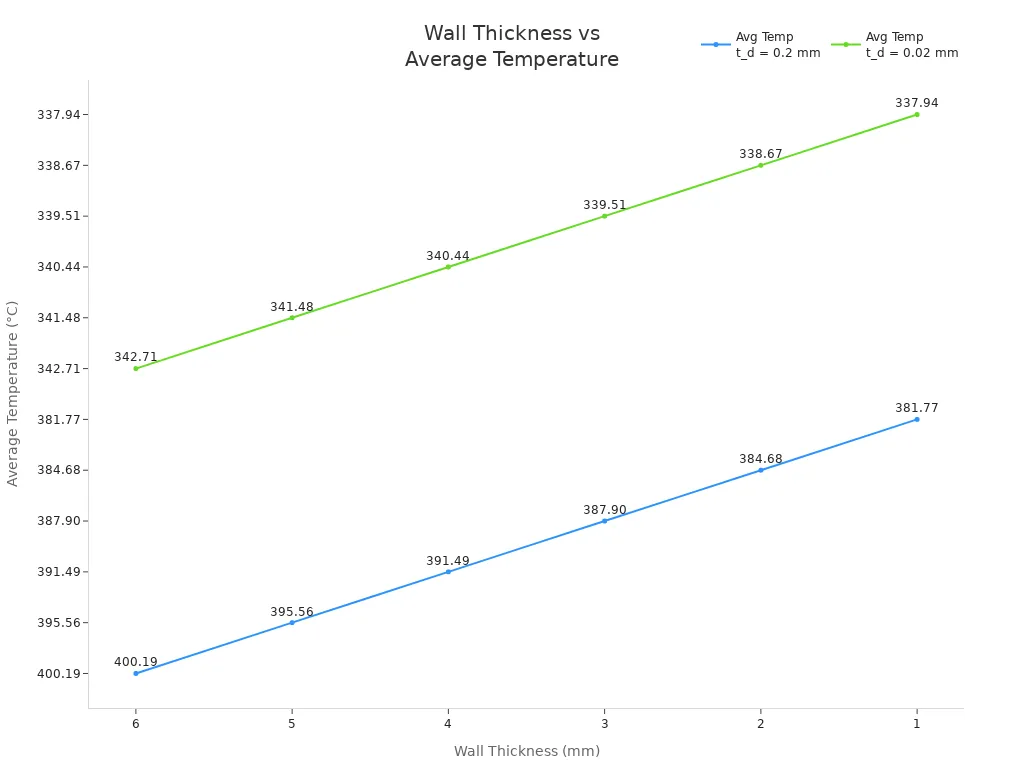
A análise dos dados do forno de laboratório mostra que os tubos com tolerâncias dimensionais mais rígidas mantêm um desempenho estável. As normas ISO e ASTM recomendam um controle rigoroso da espessura da parede para evitar gradientes térmicos que excedam os limites de segurança. A tabela abaixo demonstra como a temperatura média muda com a espessura da parede e uniformidade:
Espessura da parede (mm) | Temp. média (°C) em t_d = 0,2 mm | Temp. média (°C) em t_d = 0,02 mm |
|---|---|---|
6 | 400.19 | 342.71 |
5 | 395.56 | 341.48 |
4 | 391.49 | 340.44 |
3 | 387.90 | 339.51 |
2 | 384.68 | 338.67 |
1 | 381.77 | 337.94 |
Esses dados destacam a ligação direta entre a uniformidade da espessura da parede e o controle de temperatura. Resultados confiáveis dependem da manutenção dessas tolerâncias rigorosas.
Uniformidade da taxa de aquecimento: Impacto da espessura da parede na distribuição circunferencial da temperatura
A espessura uniforme da parede em tubos de quartzo para aplicações analíticas garante que as taxas de aquecimento permaneçam consistentes ao redor do tubo. Quando a parede é uniforme, cada seção absorve e transfere calor na mesma proporção, o que favorece a consistência e a qualidade do processo. Paredes desiguais fazem com que algumas áreas aqueçam mais rapidamente, criando desequilíbrios de temperatura e arriscando a contaminação ou a perda de pureza do SiO₂.
Análises e testes confirmam que a precisão dimensional na espessura da parede leva a um melhor desempenho em equipamentos de tolerâncias dimensionais de tubos de quartzo de laboratório. As normas ISO exigem esse nível de controle para atender aos protocolos de certificação e manter a integridade dos resultados analíticos. Os pontos a seguir resumem o impacto:
A espessura uniforme da parede evita aquecimento desigual e pontos quentes
Taxas de aquecimento consistentes garantem a qualidade do processo e reduzem a contaminação
A precisão dimensional garante desempenho e certificação confiáveis
Esses fatores mostram por que os laboratórios confiam no vidro de quartzo certificado com tolerâncias precisas para instrumentos analíticos exigentes.
Integração de fornos de várias zonas: Requisitos de aquecimento sincronizado para controle de processos
Os fornos de várias zonas dependem de tubos de quartzo com espessura de parede uniforme para sincronizar o aquecimento em todas as zonas. Quando cada zona se aquece na mesma velocidade, o controle do processo melhora e os resultados se tornam mais repetíveis. As variações na espessura da parede interrompem esse equilíbrio, fazendo com que algumas zonas fiquem atrasadas ou superaquecidas, o que afeta a precisão dos protocolos analíticos.
Um gráfico ilustra como a temperatura média diminui à medida que a espessura da parede se torna mais uniforme, o que permite um melhor controle do processo:
O vidro de quartzo com tolerâncias dimensionais certificadas atende aos padrões ISO e ASTM para integração em fornos multizonas. Os laboratórios obtêm resultados confiáveis e de alta qualidade e reduzem o risco de contaminação ou impurezas quando usam tubos com uniformidade comprovada de espessura de parede.
Como a tolerância de comprimento de ±2 mm afeta o projeto da folga de expansão térmica?
A tolerância de comprimento desempenha um papel fundamental na integração de equipamentos de tolerâncias dimensionais de tubos de quartzo de laboratório. Os engenheiros contam com uma tolerância de ±2 mm para manter as folgas de expansão adequadas, evitar o encaixe forçado e garantir o alinhamento preciso. Esse nível de controle oferece suporte a um desempenho confiável, protege contra contaminação e mantém os padrões de qualidade exigidos para instrumentos analíticos.
Cálculo da folga de expansão térmica: Crescimento de 0,54 mm que requer uma folga de 2-3 mm
Os tubos de quartzo para aplicações analíticas se expandem quando expostos a altas temperaturas. A análise mostra que um tubo de quartzo de 1000 mm cresce cerca de 0,54 mm quando aquecido de 20 °C a 1100 °C, com base no coeficiente de expansão térmica (α = 0,5 × 10-⁶ K-¹). Os engenheiros projetam uma folga de instalação de 2 a 3 mm para acomodar esse crescimento, garantindo que o tubo não seja pressionado contra as extremidades do forno.
Esse cálculo evita o estresse mecânico e mantém a integridade do sistema. Se a folga for muito pequena, o quartzo em expansão poderá causar rachaduras ou desalinhamento, com risco de contaminação e redução da pureza do SiO₂. Os testes confirmam que a manutenção da folga correta favorece a operação confiável e atende aos padrões ISO e ASTM de qualidade e certificação.
Pontos principais:
A folga de 2-3 mm evita estresse e rachaduras durante o aquecimento
A liberação correta mantém a integridade e o desempenho do sistema
A análise precisa garante a conformidade com os padrões ISO e ASTM
Prevenção de estresse na instalação: Como ±2 mm elimina o encaixe forçado (tensão de contato de 30 MPa)
A tolerância de comprimento adequado elimina a necessidade de encaixe forçado durante a instalação. Quando os tubos de quartzo atendem à especificação de ±2 mm, eles se encaixam suavemente no forno sem compressão ou vãos sem suporte. A análise revela que os tubos superdimensionados podem gerar mais de 30 MPa de tensão de contato nas extremidades, o que pode levar a rachaduras e falhas precoces.
Os engenheiros usam tolerâncias dimensionais para evitar esses riscos e garantir resultados confiáveis. O encaixe forçado não apenas danifica o vidro de quartzo, mas também aumenta a chance de entrada de impurezas no sistema. Ao seguir protocolos e padrões certificados, os laboratórios protegem a qualidade de seus instrumentos analíticos e mantêm um desempenho consistente.
Condição de instalação | Tensão de contato (MPa) | Risco de falha | Impacto na qualidade |
|---|---|---|---|
Ajuste adequado (±2 mm) | <5 | Baixa | Alto, certificado |
Ajuste forçado (+5 mm) | >30 | Alta | Baixa, contaminação |
Essa tabela destaca como as tolerâncias corretas afetam diretamente a qualidade e a confiabilidade do sistema.
Alinhamento da zona de aquecimento: Impacto da tolerância de comprimento na precisão do perfil de temperatura
A tolerância precisa do comprimento garante que os tubos de quartzo se alinhem às zonas de aquecimento do forno. Quando os tubos atendem ao requisito de ±2 mm, cada zona de aquecimento fornece uma temperatura uniforme, dando suporte ao controle preciso do processo. Tubos desalinhados podem causar aquecimento desigual, o que afeta a precisão dos resultados analíticos e pode introduzir contaminação.
Análises e testes mostram que o alinhamento adequado melhora o desempenho e a qualidade. Os laboratórios que usam vidro de quartzo certificado com tolerâncias dimensionais rígidas obtêm melhores resultados e reduzem o risco de impurezas. O alinhamento confiável também é compatível com a certificação ISO e ajuda a manter protocolos laboratoriais rigorosos.
Resumo dos benefícios:
O alinhamento preciso suporta perfis de temperatura precisos
O aquecimento uniforme melhora a qualidade e os resultados do processo
As tolerâncias certificadas reduzem a contaminação e permitem um desempenho confiável
Como a tolerância de linearidade <0,5 mm/500 mm afeta a integração do alinhamento óptico?
A tolerância de retidão em tubos de quartzo desempenha um papel fundamental no alinhamento óptico de equipamentos de laboratório. A manutenção de menos de 0,5 mm de desvio por 500 mm de comprimento garante que os caminhos da luz permaneçam precisos e confiáveis. Esse nível de controle permite resultados de alta qualidade e protege a integridade dos instrumentos analíticos.
Desvio do caminho óptico: Como a linearidade de <0,5 mm mantém o alinhamento angular de <0,3°
Os tubos de quartzo para aplicações analíticas devem manter o caminho óptico reto para evitar a perda de sinal. Quando a tolerância de retidão fica abaixo de 0,5 mm por 500 mm, o desvio angular permanece abaixo de 0,3°, o que atende aos padrões ISO para alinhamento óptico. Essa precisão garante que a luz percorra o tubo sem dobras ou dispersão significativas.
A análise mostra que mesmo pequenos desvios podem causar perdas mensuráveis na transmissão. Por exemplo, um tubo com 1 mm de arco por 500 mm pode reduzir o rendimento da luz em 5-15%, o que afeta a precisão dos resultados e pode exigir novos testes. O vidro de quartzo certificado com tolerâncias rígidas de retidão oferece suporte ao desempenho confiável em espectroscopia e sistemas baseados em laser.
Pontos principais:
Mantém o caminho óptico dentro de <0,3° para alta precisão
Reduz a perda de sinal e melhora a qualidade da medição
Oferece suporte à certificação ISO e a protocolos analíticos confiáveis
Prevenção de interferência mecânica: Tubos curvados criando espaços irregulares e infiltração de ar
Tubos de quartzo curvados podem criar espaços irregulares entre o tubo e o orifício do forno. Esse desalinhamento permite a entrada de ar, o que aumenta o risco de contaminação e reduz a pureza do SiO₂. A análise do equipamento de tolerâncias dimensionais de tubos de quartzo de laboratório mostra que a tolerância de retidão abaixo de 0,5 mm por 500 mm evita esses problemas.
Os testes confirmam que os tubos com maior curvatura geralmente apresentam taxas de infiltração de ar até 10 vezes maiores do que os tubos retos certificados. Isso pode introduzir impurezas e perturbar ambientes controlados, levando a resultados não confiáveis e à falha na certificação. A manutenção da retidão adequada também ajuda a evitar interferência mecânica, que pode danificar o tubo e o equipamento.
Condição do tubo | Taxa de Infiltração de Ar | Risco de contaminação | Impacto na qualidade |
|---|---|---|---|
<0,5 mm/500 mm | Mínimo | Baixa | Alto, certificado |
>1,0 mm/500 mm | Alta | Alta | Baixo, reteste |
Essa tabela destaca como a tolerância de retidão afeta diretamente o risco de contaminação e a qualidade geral.
Distribuição de carga de suporte: Impacto da retidão na tensão de contato e no início da fissura
Os tubos de quartzo com retidão adequada distribuem seu peso uniformemente pelos pontos de apoio. Essa carga uniforme evita a alta tensão de contato, que pode causar rachaduras durante o ciclo térmico. A análise das tolerâncias dimensionais mostra que os tubos retos reduzem o risco de falha mecânica e prolongam a vida útil do equipamento.
Quando um tubo se curva, a maior parte do peso recai sobre um ou dois pontos, aumentando a tensão local acima de 25 MPa. Essa tensão pode levar ao início de rachaduras e à falha precoce, especialmente durante ciclos repetidos de aquecimento e resfriamento. O desempenho confiável depende da manutenção da retidão dentro dos padrões certificados, o que favorece a qualidade e os resultados de longo prazo.
Tabela de resumo:
Tolerância de retidão | Estresse de contato | Risco de rachaduras | Vida útil do equipamento |
|---|---|---|---|
<0,5 mm/500 mm | Baixa | Baixa | Estendido |
>1,0 mm/500 mm | Alta | Alta | Reduzido |
A tolerância adequada de retidão no vidro de quartzo garante uma operação segura e apoia a precisão dos instrumentos analíticos.
Como o empilhamento de tolerância combinada afeta a integração de equipamentos em nível de sistema?
A integração de equipamentos em nível de sistema depende de como as tolerâncias dimensionais se acumulam em vários componentes. Os engenheiros precisam entender como essas tolerâncias interagem para manter o ajuste da montagem, a confiabilidade e a qualidade do sistema. A análise e a especificação cuidadosas ajudam a evitar a contaminação, garantem a certificação e apoiam o desempenho confiável dos equipamentos de tubos de quartzo de laboratório.
Análise de tolerância estatística: Método RSS para cálculo de empilhamento multidimensional
A análise estatística de tolerância ajuda os engenheiros a prever como as tolerâncias dimensionais múltiplas se combinam em uma montagem real. O método Root Sum Square (RSS) calcula a variação total provável, considerando a distribuição de cada tolerância, em vez de simplesmente somar os extremos. Essa abordagem fornece uma estimativa mais realista do empilhamento total, apoiando melhores decisões de projeto para tubos de quartzo para aplicações analíticas.
Os engenheiros usam o método RSS para avaliar o efeito combinado das tolerâncias de diâmetro externo, espessura da parede, comprimento e linearidade. Por exemplo, se um sistema tiver diâmetro externo de ±0,2 mm, parede de ±0,1 mm, comprimento de ±2 mm e retidão de 0,5 mm, o cálculo do RSS será √(0,2² + 0,1² + 2² + 0,5²) ≈ 2,1 mm. Esse valor prevê a variação efetiva no sistema montado, ajudando a manter a qualidade e a reduzir o risco de contaminação ou desalinhamento. A análise estatística é compatível com os padrões ISO e garante que os componentes de vidro de quartzo atendam aos protocolos de certificação.
Pontos principais:
A análise de RSS prevê uma variação total realista nas montagens
Ajuda a manter o ajuste e a qualidade do sistema, evitando o empilhamento excessivo
Oferece suporte a requisitos de certificação e ISO para resultados confiáveis
Pior caso vs. empilhamento estatístico: Implicações do projeto de liberação do sistema
As análises de pior caso e de empilhamento estatístico oferecem abordagens diferentes para prever as necessidades de folga do sistema. A análise do pior caso usa os valores máximos ou mínimos de cada tolerância, garantindo que até mesmo a combinação mais extrema será adequada. A análise estatística, como a RSS, considera a probabilidade de variações, fornecendo uma estimativa mais prática para a maioria das montagens.
Os projetistas geralmente comparam esses métodos para equilibrar o risco e a capacidade de fabricação. A análise do pior caso pode levar a folgas muito grandes e a custos mais altos, enquanto a análise estatística permite projetos mais rígidos e eficientes. A tabela abaixo destaca as principais diferenças entre essas duas abordagens e seu impacto na integração em nível de sistema.
Aspecto | Análise do pior caso | Análise estatística |
|---|---|---|
Abordagem das tolerâncias | Usa valores máximos ou mínimos para calcular os extremos de folga ou interferência. | Avalia valores com base na probabilidade e na distribuição de variações, como RSS ou Monte-Carlo. |
Foco | Lida com os limites de aceitabilidade sem considerar a probabilidade. | Concentra-se na distribuição de variações e nas previsões reais de montagem com base nas dimensões das peças. |
Entradas | As tolerâncias de projeto são os principais insumos. | Os momentos de distribuição do processo (por exemplo, desvio padrão) são as entradas principais. |
Essa comparação mostra que a análise estatística geralmente leva a projetos de sistemas mais precisos e econômicos, enquanto a análise do pior caso maximiza as margens de segurança, mas pode aumentar os custos de material e fabricação.
Análise de custo-benefício da integração: Prêmio de tolerância apertada vs. economia de retrabalho
A especificação de tolerâncias dimensionais mais rígidas aumenta os custos iniciais de produção, mas pode reduzir a necessidade de retrabalho e melhorar a qualidade geral do sistema. Os engenheiros devem pesar o custo de uma inspeção mais rigorosa e a possibilidade de sucata em relação à economia decorrente de menos falhas de integração e menos contaminação. Dados de testes e de campo mostram que as tolerâncias mais rígidas geralmente se pagam em montagens complexas.
Por exemplo, os tubos de quartzo com tolerância de ±0,1 mm custam mais para serem produzidos devido ao aumento da inspeção e aos controles de fabricação mais rígidos. No entanto, esses tubos reduzem o risco de impurezas, melhoram a pureza do SiO₂ e oferecem suporte ao desempenho confiável em instrumentos analíticos. A tabela abaixo resume o impacto do custo de diferentes níveis de tolerância:
Tolerância | Impacto nos custos | Notas |
|---|---|---|
±0,1 mm | ↑ Custo | Aumento da inspeção e possível sucata devido a tolerâncias mais rígidas |
Resumo dos benefícios:
Tolerâncias mais rígidas reduzem o retrabalho e melhoram a qualidade do sistema
Custos iniciais mais altos podem resultar em economia a longo prazo
O vidro de quartzo certificado oferece resultados confiáveis e certificação ISO
A análise cuidadosa e a especificação das tolerâncias dimensionais ajudam os laboratórios a obter uma integração confiável e de alta qualidade, além de controlar os custos e manter a integridade do sistema.
Como os engenheiros devem especificar as tolerâncias dimensionais para obter sucesso na integração de equipamentos?

Os engenheiros precisam combinar as tolerâncias dimensionais com as necessidades específicas dos equipamentos de laboratório. A seleção cuidadosa garante que os tubos de quartzo para aplicações analíticas ofereçam desempenho confiável e resultados consistentes. Métodos adequados de análise e verificação ajudam a evitar a contaminação e a manter a alta qualidade.
Matriz de seleção de tolerâncias: Correspondência entre especificações dimensionais e requisitos de integração de equipamentos
Os engenheiros começam identificando as interfaces críticas em seu sistema, como superfícies de vedação, pontos de apoio e caminhos ópticos. Eles selecionam as tolerâncias com base no desempenho necessário para cada aplicação. Por exemplo, os sistemas selados a vácuo exigem tolerâncias mais rígidas de diâmetro externo e espessura de parede para evitar vazamentos e reduzir as impurezas.
A análise dos dados de fabricação mostra que os tubos de quartzo com tolerância de ±0,1 mm para o vidro de quartzo de camada dupla e de ±0,15 mm para o vidro de quartzo transparente cilíndrico são os mais adequados para aplicações de alta precisão. O teste de vazamento, conforme descrito na norma ASTM C657, verifica se essas tolerâncias evitam a contaminação e mantêm a pureza da amostra. Os fabricantes também usam testes de queda de pressão e de vazamento de hélio para confirmar a integridade da vedação e garantir uma operação confiável.
A tabela a seguir resume as tolerâncias recomendadas e os métodos de verificação para diferentes tipos de tubos de quartzo, destacando a ligação entre especificação e qualidade:
Tipo de tubo de quartzo | Tolerância | Método de verificação | Impacto na qualidade |
|---|---|---|---|
Vidro de quartzo de camada dupla | ±0,1 mm | Teste de vazamento/hélio | Alta, evita impurezas |
Vidro cilíndrico de quartzo transparente | ±0,15 mm | Teste de queda de pressão | Confiável, reduz o ruído |
A seleção das tolerâncias e dos métodos de verificação corretos garante que os tubos de quartzo atendam aos rígidos padrões de qualidade. Essa abordagem oferece suporte a um desempenho consistente, reduz o risco de contaminação e fornece resultados confiáveis em ambientes laboratoriais.
As tolerâncias dimensionais determinam a qualidade e o desempenho dos tubos de quartzo para aplicações analíticas. Os laboratórios dependem de dimensões precisas de quartzo para evitar contaminação e garantir resultados confiáveis. A adequação das tolerâncias a cada aplicação - seja para vedação a vácuo, controle térmico ou alinhamento óptico - protege contra impurezas e garante uma qualidade consistente. Os engenheiros podem melhorar os resultados trabalhando em estreita colaboração com fornecedores que usam usinagem avançada de quartzo e seguindo as práticas recomendadas para verificação.
Aspecto da colaboração | Descrição |
|---|---|
Manufatura avançada | Retificação CNC com diamante para tolerâncias estreitas em vidro de quartzo |
Parcerias de engenharia | Especialistas otimizam a seleção e o design do quartzo |
Colaboração técnica | Suporte direto para melhorias de projeto e processo |
Exigir que os fornecedores forneçam relatórios de impureza e teor de hidroxila.
Use anéis O-ring duplos e testes de vazamento com hélio para reduzir a contaminação.
Pré-cozinhe ou limpe com ácido os tubos de quartzo antes dos experimentos.
PERGUNTAS FREQUENTES
Por que os laboratórios exigem tolerâncias rígidas de diâmetro externo para tubos de quartzo?
As tolerâncias rígidas de diâmetro externo garantem uma vedação adequada em sistemas de vácuo. Isso evita vazamentos e contaminação. As vedações confiáveis protegem experimentos sensíveis e mantêm o desempenho do equipamento.
Por que a uniformidade da espessura da parede é importante em aplicações de fornos?
A espessura uniforme da parede permite a transferência uniforme de calor. Isso evita pontos quentes e reduz o estresse térmico. O aquecimento consistente melhora o controle do processo e aumenta a vida útil do tubo.
Por que a linearidade é importante para o alinhamento óptico?
Os tubos retos mantêm o caminho óptico preciso. Isso minimiza a perda de sinal e os erros de medição. A retidão adequada permite resultados de alta qualidade em sistemas de espectroscopia e laser.
Por que os engenheiros devem usar a análise de tolerância estatística?
A análise estatística prevê a variação da montagem no mundo real. Isso ajuda os engenheiros a projetar folgas que evitam interferências ou lacunas. Isso reduz o retrabalho dispendioso e melhora o sucesso da integração.
Por que uma tolerância mais rígida aumenta o custo inicial, mas reduz a despesa total?
As tolerâncias mais rígidas exigem fabricação e inspeção avançadas. Isso aumenta os custos iniciais. Entretanto, menos falhas de integração e menos retrabalho economizam dinheiro ao longo do tempo.